How Galilean Relativity And The Lorentz Maxwell Equations (The 2 Postulates) Contradict

Now we have to see how both peoples coordinates relate to each other's. 

Person B's position is X' = 0 and person A's position is X = 0. Distance = Speed x Time. Therefore we can say

Person B's position (X') is the difference between person A's positon (X) and the distance between persons A and B.

Imagine you standing in a field and your friend is 100m away. If you say you are at 0m and your friend is 100m away you can say your friend's position is the difference between your position (0m) and the gap between you two (100m).

X' = X - the distance between person's A and B

X' = X - vt where v is speed.

We also assume that everyone records time in the same way.

Person A's recordings of time = Person B's recordings of time

Person A's recording of time is already t but lets just call person B's recording of time t'

t = t'

From theses two equations both people can say when and where events happen in the other persons frame of reference.

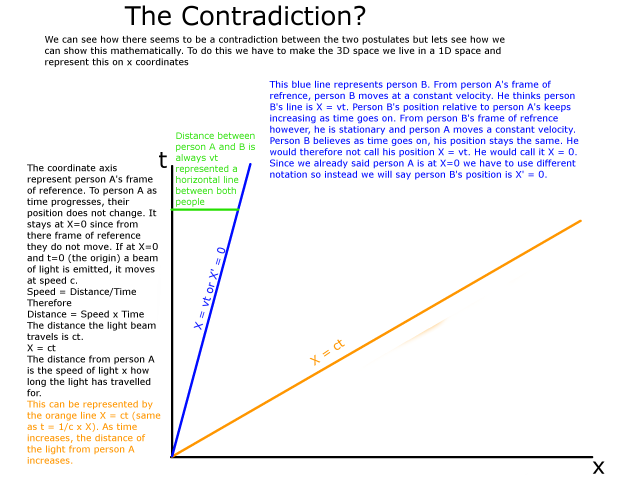
We know that the light rays position is X = ct.

Since X' = X - vt

we can substitute in ct for X and get

X' = ct - vt

X' = (c - v)t

and since both people measure time in the same way

X' = (c - v)t'

This equation means that unlike person A who sees light moving at speed ct. X = ct

Person B sees light moving slowly at speed c - v. X' = (c - v)t'

This makes intuitive sense because person B moves in the same direction as the light and so should see it move slower. This is the same as if you are driving in a car and get overtaken. You would see the car passing you move slower than someone who was in a stationary frame of reference.

We could also imagine a light ray that was shone in the other direction. This would have the postion X = -ct

If we substitute in -ct we get

X' = -ct - vt

X' = -(c + v)t

X' = -(c + v)t'

This equation means that person B sees light moving quicker than c at c + v.

This again makes sense as if you were driving past a car going in the opposite direction it would seem to move faster than to someone who was standing stationary on the roadside.

This contradicts the 2nd postulate however. People had realised that no matter how things moved the speed of light would always be measured at c. Einstein therefore realised that was something was wrong in the way we transformed the coordinates of the two people. 

Another way we can use the graph to see that the observers supposedly measure light at different speeds is by rotating the graph. We know we can say person B is stationary and we can say that he can have his own graph where his line is rotated anticlockwise to become vertical. This is because it would represent him stationary at the point X' = 0 and seeing person B changing position (moving at a constant velocity). While rotating his line, we would also have to rotate the line X = ct at the same angle that person B's line was rotated by. We would then clearly be able to see that the line representing light is steeper. This would mean it is travelling a shorter distance over a longer time meaning the speed of light from person B's frame of reference is slower.

The lights total velocity is a combination of the speed of light that Person A witnesses and the velocity of the train moving that person B sees.

The train moves horizonatally at speed v. The light moves vertically at speed c. Calling the speed of light that person B sees c', pythagoras's theorem shows that the total diagonal speed of the light is

v² + c² = c'²

c' = √(v² + c²)

The train is definitely moving and so c' will be greater than c (the speed of light recorded by person B). 

This is another example where the two postulates seemingly contradict. Something must have gone wrong since both observers should be measuring light at the same speed.

Thanks for reading and I encourage you to leave comments about your thoughts on the topic, things I haven't covered in this post, how you think I can improve my posts, what you liked about this topic etc..

If you enjoyed this post or any of my others, follow this blog.

Be sure to also share this around with your friends and family.