What's 1 + 2 + 3 + 4 + 5 + 6 + 7 + ... + 1000 (Solve In Less Than 5 Seconds!)

What's 1 + 2 + 3 + 4 + 5 + 6 + ... + 1000

So how can we go about calculating this?
Obviously, there is the brute force method of adding up 1000 numbers; but surely there is a trick that lets us do this quickly?

The key is pairing the numbers.
If we pair 1 with 1000 giving 1001
2 with 999 giving 1001
3 with 998 giving 1001
and so on…
We eventually have 500 pairs of numbers all adding up to 1001
From there its a simple job of multiplying 500 with 1001 to give 500500

Easy

Another way to think about this problem is pairing all the numbers then dividing them by 2.
This gives the average value of each number (500.5 in this case)
If we then multiply the average value of each number (500.5) by the total number of numbers (1000) we again get 500500.

We can do this trick for any arithmetic sequence (a sequence where the difference between the numbers is constant). As long as we know the first number, the last number and how many numbers are in the sequence.
For example, 2 + 4 + 6 + 8 + …. + 500000
3 + 6 + 9 + 12 + … + 99999
5 + 12 + 19 + 26 + …. + 705

So can we get a general formula which lets us calculate the sum of any series?

Lets define a as the first term in a sequence
d as the common difference between the numbers in the sequence
n as the number of terms in the sequence
The sequence would go as follows

a + a + d + a + 2d + a + 3d + a + 4d + a + 5d + … + a + (n-1)d

You may wonder why the last term is a + (n-1)d and not a + (n)d but consider the third term.
This is a + 2d, not a + 3d, and so we can see the number before d is always one less than its corresponding term number.

Lets now find the average value of the numbers in the sequence.

The first term is a, the last term is a + (n-1)d
To get the average we add the first and last term and then divide by two giving


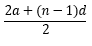
All we need to do now is multiply the average value by the total number of terms - n
and this gives


And this formula tells us how to add up any arithmetic sequence where
n is the number of terms in the sequence
a is the starting value
d is the common difference between each term


We can also get this formula by pairing the terms.
We can pair the first and last terms giving

a + a + (n-1)d
=> 2a + (n-1)d

We then multiply this by half of the number of terms (since each pair contains 2 numbers) - n/2
And this gives us the same formula