Polarization At An Arbitary Angle

Thursday, November 22, 2018

Polarization At An Arbitary Angle

Polarization

In the previous post on quantum mechanics, we went through the steps to describe the polarization of a photon at some simple angles. In this post, we will try to extend this to include photons polarized at any angle.

Photons At An Arbitrary Angle

How can we describe photons polarized at an arbitrary angle? If we have two polarizers at angles θ and θ + 90°,
1. How will we describe the photons which pass through the polarizers?
2. What is the hermitian operator corresponding to the observable?

If you pass through the polarizer at an angle θ, you get the eigenvector |θ>
If a photon passes through the polarizer at the θ + 90° angle, it can be described by the eigenvector |θ + π/2> (note π/2 is the same as 90° in a different unit called radians)

The justification of the following is experimental but the results show that these photons can be described as the following vectors.
|θ> = cosθ|x> + sinθ|y>

|θ + π/2> = cos(θ + π/2)|x> + sin(θ + π/2)
= -sinθ|x> + cosθ|y>

We can check these are normalised by performing the inner product of one vector with itself and squaring the modulus of the result. This is because this is the probability that a photon goes through a polarizer at the angle of the eigenvector should be 1. (Remember the ket vectors should be column vectors but I can't write these on blogger).
<θ|θ>
= (cosθ<x| + sinθ<y|) (cosθ|x> + sinθ|y>)
= cos²θ + sin²θ
We then square the modulus of the result (but this does nothing here as 1 squared is still 1)
cos²θ + sin²θ = 1
And since the result is 1, the vectors are normalised already. We can also check the other eigenvector and we will arrive at the same result.

We can also check if they are orthogonal by taking the inner product of the two eigenvectors.
<θ|θ + π/2>
(cosθ<x| + sinθ<y|) (-sinθ|x> + cosθ|y>)
= -cosθsinθ + sinθcosθ)
= 0

This means we have another basis for our space of states. These are two orthogonal and normalized vectors. So if we have a photon polarized along θ, what's the chance of it going through our x or y polarizers?

Probablity it goes through x polarizer = | <x|θ> |²
<x|θ> = cosθ

| <x|θ> |² = cos²θ

Probablity it goes through y polarizer = | <y|θ> |²
<y|θ> = sinθ

| <x|θ> |² = sin²θ

And the photon has to be able to go through the x or y polarizer and so the sum of these must be 1 (which they are).

You can observe polarization at these angles and so polarization in the θ direction should have an hermitian operator. It should do the following

P|θ> = |θ>
P|θ + π/2> = -|θ + π/2>

This is the appropriate matrix corresponding to observing the polarization of a photon at an arbitrary angle

Let's try something else. If we create a photon polarized along an arbitrary angle α, what's the probability that it goes through a polarizer put at an angle β. This will depend on the angle difference between the two polarizers. A photon polarizsed along α can be described as the following vector.
|α> = cosα|x> + sinα|y>

When we test for polarization along the angle β, the photon that emerges will be described by the following vector
|β> = cosβ|x> + sinβ|y>
We can also write this as a bra vector and as a row vector
<β| = (cosβ, sinβ)

The probability of the photon passing through is calculated by taking the inner product to get the amplitude and squaring it.
<β|α> = cosαcosβ + sinαsinβ (And from the double angle formula this can be rewritten as)
=cos(α - β)

Probability of passing second polarizer = | <β|α> |²
=cos²(α - β)

This probability makes sense because if α = β it is 1. If the polarizers are in the same direction, all photons should pass through the second if they make it past the first.
As β increases, the probability decreases and when α - β = π/2, the probability is 0. This makes sense because if the 90°

Strange Quantum Mechanics

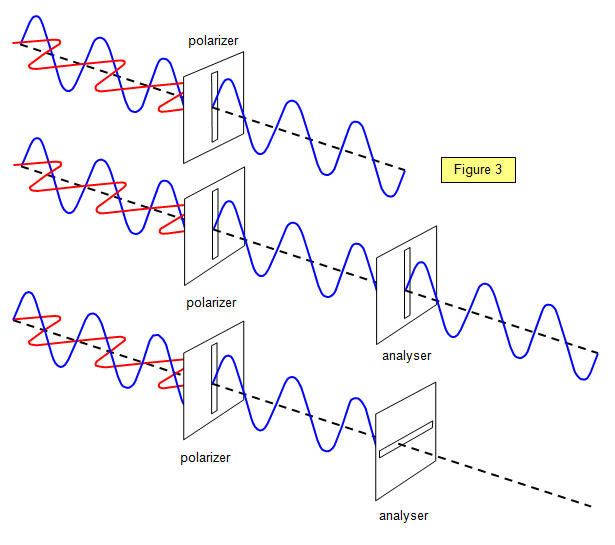
A strange result in polarization experiments is that when two perpendicular polarizers are placed in a line, no light will get through the 2nd. If you then insert a 3rd polarizer inbetween the 2 polarizers, you end up with more light getting through. In classical physics, putting an obstacle in the way resulting in more light getting through would be pretty crazy. In quantum mechanics, this kind of stuff can happen and we can show this mathematically.

We have a polarizer at the angle θ, then a horizontal polarizer and then a polarizer at angle θ + 90°.

What is the probability that a photon polarized at θ gets through the x polarizer?
We already worked out that this was cos²θ.

Now it is polarized in the horizontal direction, what chance does it have of making it through the third polarizer? This depends on the angle difference and we just worked out the formula for this
Probability = cos²(α - β) where α = 0 and β = θ + π/2
= cos²(- θ - π/2)
= cos²(θ + π/2)
= 1 - sin²(θ + π/2)
= 1 - sin(θ + π/2)sin(θ + π/2)
= 1 - (sinθcosπ/2 + cosθsinπ/2)(sinθcosπ/2 + cosθsinπ/2)
= 1 - cosθcosθ
= 1 - cos²θ.

= sin²θ

And so the probability of a photon polarized at an angle θ making it through the horizontal and θ + polarizes 90°is gotten by multiplying our probabilities.

This is cos²θsin²θ which is greater than or equal to 0 and so putting an extra filter does increase the chance of getting through...

Where Are The Imaginary Numbers?

You may be wondering where are imaginary numbers?

What would a state vector (as a bra/row vector) of (1, i) mean?

Firstly this is not normalized. The vector multiplied by its complex conjugate should equal one but

1 x 1 + i x -i

= 1 + 1

= 2

So to normalize it we need to divide by √2.

1√2(1,i) = 1/√2 |x> + i/√2 |y>

There is also a vector orthogonal to this

1/√2(1, -i) = 1/√2 |x> - i/√2 |y>

And we can confirm this is orthogonal by taking the inner product of the vectors.

This also means there is an observable that can distinguish the two vectors. It turns out that these vectors correspond to circularly polarized light, where these photons have a 50% chance of going through any plane polarizer (can check this by taking the inner product and multiplying it by its complex conjugate).

Circularly polarized light is where the magnitude of the electric field is constant, but rotates over time at a steady rate in a plane perpendicular to direction of wave.

From here the maths gets a lot more complicated so at a later date, I will revisit polarization and start to go into detail about circularly and elliptically polarized photons...

Thanks for reading. If you enjoyed this post or any of my others, follow and subscribe to my blog. Feel free to discuss anything related to this post or ask questions in the comments below.