Relativistic Kinetic Energy (Integration By Parts)

Monday, October 15, 2018

Relativistic Kinetic Energy (Integration By Parts)

Relativistic Kinetic Energy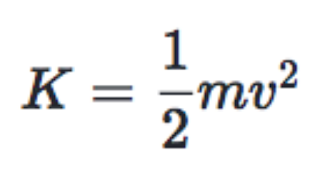

Now we know the relativistic momentum equation, we can derive the relativistic kinetic energy equation. This is another formula which is different from what we are taught at school when doing classical mechanics.

The change in kinetic energy a particle experiences is the same as the work done to it
𐤃KE = Work Done

𐤃KE = F𐤃x

𐤃KE = dp/dt 𐤃x

𐤃KE = dp 𐤃x/dt (a change in distance over a tiny change in time (dt) is a velocity)

𐤃KE = dp v

p = mvγ

𐤃KE = d(mvγ) v
d KE = v d (mvγ)
And now integrating this expression gives the kinetic energy formula
∫ d KE = KE

KE = ∫ v d (mvγ)

This integral gives (see the derivation at the end of the post)

KE = mc²(γ - 1)

As v increases, gamma approaches infinity. This means KE approaches infinity and so to accelerate an object to the speed of light, you would require infinite energy. This again shows that objects with mass can never reach the speed of light since as speed increases, it gets harder to accelerate them and so you would need infinite energy.

The equation also shows that kinetic energy is made up of a term that depends on the objects speed and one that is a constant for the object.
KE = mc²γ - mc²

You might interpret it as
Kinetic Energy = Total Energy - Rest Energy
Total Energy = mc²γ
Rest Energy = mc²
This is strongly hinting at E = mc².

We are now one step away from Einstein's famous equation. The next post on special relativity will show the full derivation using our new knowledge on kinetic energy, momentum and velocity addition.

Derivations Of The Relativistic Kinetic Energy Formula

This first derivation requires knowledge of the product rule and the chain rule. There is a second derivation below which only requires integration by parts and is a lot more direct.

This is the second derivation of the formula. This one is much quicker and direct but requires knowledge of integration by parts.

Thanks for reading. If you enjoyed this post or any of my others, follow and subscribe to my blog. Feel free to discuss anything related to this post or ask questions in the comments below.